Fähigkeitsindizes geben Auskunft darüber, wie gut ein Prozess die Anforderungen erfüllt. Dies kann nur beurteilt werden, wenn der Prozess stabil ist. Die Prozessstabilität gibt an, ob ein Prozess als beherrscht oder nicht beherrscht angesehen wird. Ohne Stabilität ist die Betrachtung von Fähigkeitsindizes nicht sinnvoll. Nach ISO 25514 sind Prozesse beherrscht, wenn sich die Merkmalswerte praktisch nicht oder nur in bekannter Weise oder innerhalb bekannter Grenzen ändern. Werden zu einfache Zufallsstichproben aus dem Prozess gezogen, dann verhalten sich diese so, als kämen sie aus derselben Grundgesamtheit.
Die Berechnung der Prozessfähigkeit basiert oft auf der Annahme, dass die Prozessdaten normalverteilt sind. Von daher ein kleiner Statistikexkurs: Bei kontinuierlichen Prozessen können die Merkmalswerte jeden beliebigen Wert annehmen. Ein Beispiel ist die Temperatur in einer Maschine. Die Normalverteilung wird durch zwei Kenngrößen bestimmt. Der arithmetische Mittelwert und die Standardabweichung. Beide Kenngrößen werden aus einer Stichprobe geschätzt.
In diesem Beitrag werden die in der folgenden Abbildung dargestellten Begriffe verwendet. In einzelnen Normen oder Spezifikationen können die Bezeichnungen der einzelnen Parameter abweichen.
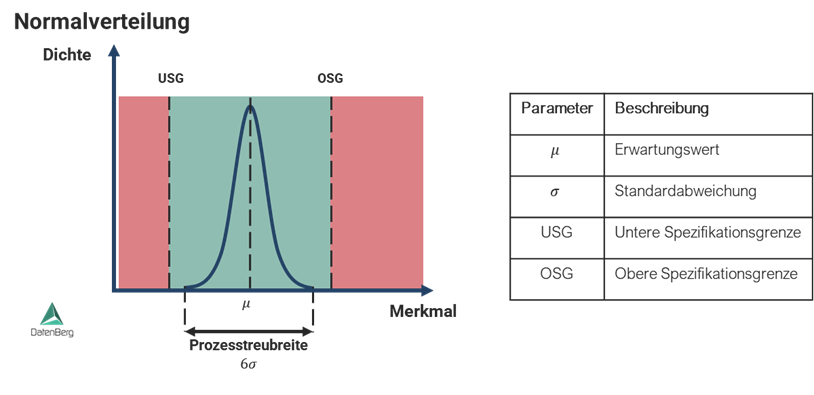
Wenn ein Merkmal normalverteilt ist, kann die Standardabweichung verwendet werden, um abzuschätzen, wie viele produzierte Teile innerhalb oder außerhalb der spezifizierten Toleranzen liegen. Unter ppm versteht man die Anzahl der Teile pro Million.
| Standardabweichung | Anteil innerhalb der Toleranz | Anteil Außerhalb der Toleranz |
|---|---|---|
| +/- 1sigma | 68,27 % | 31,73% |
| +/- 2sigma | 95,45 % | 4,55 % |
| +/- 3sigma | 99,73 % | 0,27 % |
| +/- 4sigma | 99 936 ppm | 63 ppm |
| +/- 5sigma | 999 999,43 ppm | 0,57 ppm |
| +/- 6sigma | 999 999 998 ppm | 0,002 PPM |
Der Prozessfähigkeitsindex (eng. Process capability index) gibt die Fähigkeit eines Prozesses an. Er beschreibt, inwieweit ein Prozess geeignet ist, ein Produkt herzustellen, das die Anforderungen an das Produkt erfüllt. Umgangssprachlich kann man sagen, dass die Prozessfähigkeit angibt, „wie gut der Prozess in die Toleranz passt“. Der Prozessfähigkeitsindex wird auch als „potenzieller Prozessfähigkeitsindex“ bezeichnet. Für die Berechnung des Prozessfähigkeitsindex werden zwei Spezifikationsgrenzen benötigt, eine untere und eine obere.
Für die Berechnung von cp verwendet die ISO 25514 die Schreibweise des 99,865-%-Quantil, X99,865 % und vom 0,135-%-Quantil, X0,135 %. Bei einem normalverteilten Messmerkmal kann dies als sechsfache Standardabweichung 6σ, oder 6s, angegeben werden, wenn σ aus einer Stichprobe geschätzt wird.
c_p = \cfrac{OSG - USG }{6\sigma}Der kleinste Prozessfähigkeitsindex (eng. Minimum process capability index) wird auch kritischer Prozessfähigkeitsindex genannt. Er gibt das Verhältnis von Toleranz zu Prozessstreuung unter Berücksichtigung der Prozesssituation an. Er beschreibt die Prozessfähigkeit in Bezug auf die gegebenen Spezifikationsgrenzen.
Die kritische Prozessfähigkeit wird wie folgt berechnet:
c_{pk} = min{(c_{pku},c_{pkl})} \\c_{pku} = \cfrac{\={x} - USG }{3\sigma} \\ \\ \newlinec_{pkl} = \cfrac{OSG- \={x}}{3\sigma}Bei der Bewertung der Fähigkeitsindizes können drei Phasen unterschieden werden. Vor dem Serienanlauf wird die Kurzzeitfähigkeit betrachtet. Hier stehen maschinenbedingte Einflüsse im Vordergrund. Dies kann z.B. bei der Abnahme einer Maschine erfolgen. In der vorläufigen Prozessfähigkeitsuntersuchung werden alle in der Produktion relevanten Einflussgrößen berücksichtigt. In der Langzeit-Prozessfähigkeitsuntersuchung werden die Einflüsse in der Produktion über einen längeren Zeitraum betrachtet.
| Kurzzeitfähigkeits-untersuchung | Vorläufige Prozessfähigkeits-untersuchung | Langzeitprozess-fähigkeitsuntersuchung | |
|---|---|---|---|
| Wann? | Vor Serienstart | Vor Serienstart | Analyse in der Serienproduktion |
| Fähigkeitsindex | Cm | Pp | Cp |
| Kritischer Fähigkeitsindex | Cmk | Ppk | Cpk |
Ein Produktionsprozess ist dann beherrscht, wenn sich die Verteilung der Merkmalswerte, die sich praktisch nicht oder nur in bekannter Art und Weise oder innerhalb bekannter Grenzen ändern.
Statistische Tests geben eine analytische Auskunft, ob ein Messmerkmal normalverteilt ist. Hierzu wird der p-Wert des statistischen Tests betrachtet. Ist dieser größer, als ein vorher definierter Wert (oft p=0,05) wird eine Normalverteilung angenommen. Als Test findet zum Beispiel der Kolmogorov-Smirnov Test Anwendung. Als visuelle Einschätzung kann auch ein Histogramm helfen. Für die automatisierte Berechnung bietet zum Beispiel smartPLAZA eine automatische Durchführung der statistischen Tests an.
Hier empfiehlt die DIN ISO 22514, dass obere und untere Prozessfähigkeitsindizes getrennt berechnet und betrachtet werden sollen. Hier soll nicht nur der kleinere Wert als kritischer Index angegeben werden. An beide Werte können jedoch verschiedene Anforderungen gestellt werden.
Liegt nur eine Spezifikationsgrenze (obere oder untere) vor, werden die Indizes wie oben beschrieben berechnet. Für die Angabe von kritischen Prozessfähigkeitsindizes wird jedoch kein Minimum aus den Werten für die obere bzw. untere Spezifikationsgrenze gebildet, sondern nur ein Wert angeben.
Die beiden Werte Prozessfähigkeit cp und kritische Prozessfähigkeit cpk sollten stets zusammen analysiert werden. Ist der cp-Wert viel Größer als der cpk-Wert, deutet dies auf Optimierungspotential im Prozess hin. Ein cpk-Wert von größer als 1,33 wird in der Regel als sicher eingestuft. Die individuellen Schwellwerte sind jedoch mit dem Kunden abzustimmen.
Standardnorm für Fragen zu Prozessfähigkeitsindizes: DIN ISO 22514-1:2016-08 hier zu finden
Handbuch für SPC: Statistical Process Control (SPC-3) der Automotive Industry Action Group AIAG hier zu finden
